形式論理学についての解説の記事です.
ここでは複数の命題が組み合わされた複雑な論証について解説します.
複雑な論証
論証は根拠となる命題から結論となる命題を導く,\(A\Rightarrow B\)というものでした.
他方で,実際は根拠となる命題は複数あることが一般的です.
\(A_1\)であり,\(A_2\)であり,…,\(A_n\)ならば\(B\).
命題が連鎖的につながっている場合もあります.
\(A\)であるならば\(B\),\(B\)であるならば\(C\),したがって\(A\)であるならば\(C\).
このように,命題のいろいろな結合について考察することができます.
命題の結合については「命題論理」において考察します.
複雑な論証の例
複雑な論証の例をあげていきます.
Aさんは雨天時にはバスで出勤する.今日は雨が降っている.したがって,Aさんは今日はバスで出勤する.
上記は\(A\)であり,\(B\)であるならば\(C\)であるという,並列的な例です.
雨天時にはAさんはバスで出勤するが,Aさんがバスで出勤するときは職場に早く到着する,したがって雨天時にはAさんは職場に早く到着する.
上記は\(A\)ならば\(B\),\(B\)ならば\(C\),したがって\(A\)ならば\(C\)の例です.
複雑な論証の図示
複雑な論証をわかりやすく図に示す方法があります.
\(A\),\(B\)ならば\(C\)
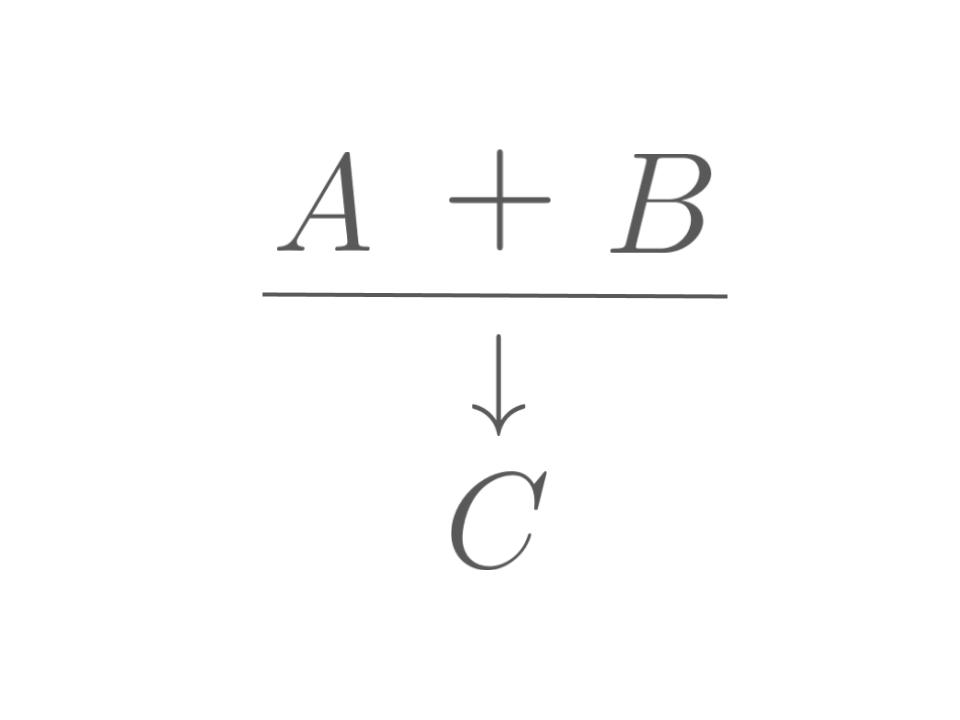
\(A\)ならば\(B\),\(B\)ならば\(C\),したがって\(A\)ならば\(C\).
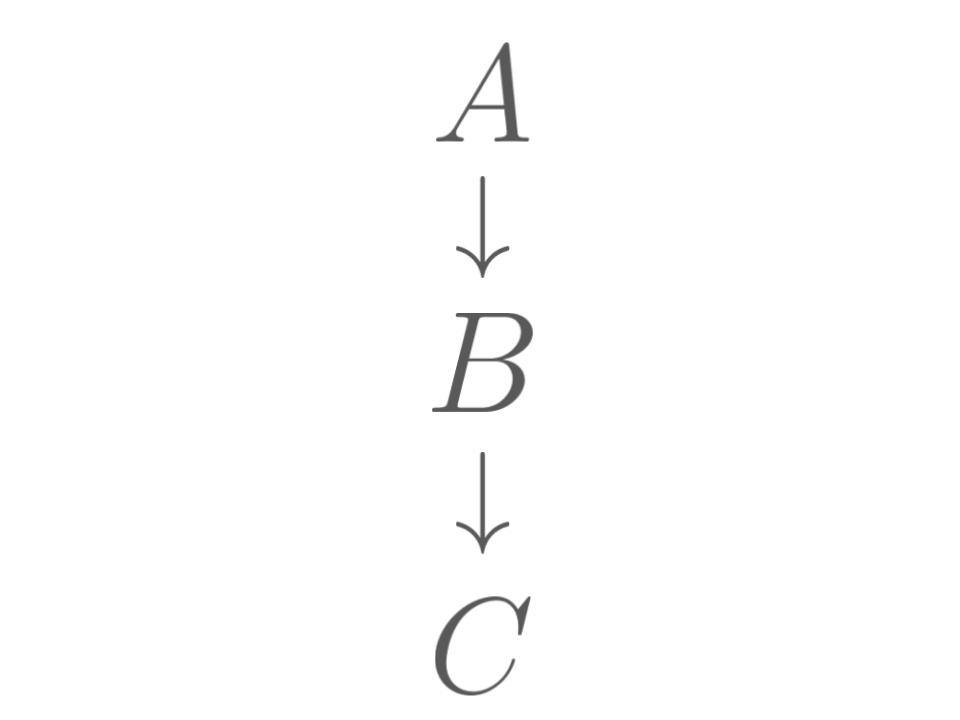
これらを組み合わせた複雑な論証も考えることができます.
参考文献
参考文献を紹介します.
以下はアフィリエイト広告です.
野矢茂樹著,『論理学』
リンク
長岡亮介著,『論理学で学ぶ数学』
リンク

