集合の包含関係は、集合論の基礎的な概念の一つで、集合間の要素の関係を定式化する重要な関係です。ここでは、包含関係の定義、性質、応用について詳しく解説します。
包含関係の定義
集合 \(A\) と集合 \(B\) について、次のように定義します:
- 部分集合(包含関係)
集合 \(A\) のすべての要素が集合 \(B\) に含まれているとき、\(A\) は \(B\) の部分集合であると言います。これを次のように記号で表します:\(A \subseteq B\)すなわち、任意の \(x\) が \(A\) に含まれるならば、\(x\) は必ず \(B\) にも含まれるということです。\(A \subseteq B \leftrightarrow \forall x(x \in A \rightarrow x \in B)\) - 真部分集合
\(A \subseteq B\) かつ \(A \neq B\) の場合、\(A\) は \(B\) の真部分集合と呼ばれます。これは、\(A\) のすべての要素が \(B\) に含まれているが、\(A\) が \(B\) と完全に等しいわけではないことを意味します。真部分集合は次の記号で表されます:\(A \subset B\) - \(A = B\) である場合は、真部分集合とは言えません。
包含関係の性質
包含関係にはいくつかの基本的な性質があります。これらの性質は、集合を扱う上で重要な役割を果たします。
- 反射律
任意の集合 \(A\) に対して、\(A\) は自分自身の部分集合です:\(A \subseteq A\) - 推移律
集合 \(A\)、\(B\)、\(C\) について、もし \(A \subseteq B\) かつ \(B \subseteq C\) ならば、必ず \(A \subseteq C\) です:\(A \subseteq B \quad \text{かつ} \quad B \subseteq C \quad \rightarrow \quad A \subseteq C\) - 反対称律
集合 \(A\) と \(B\) について、もし \(A \subseteq B\) かつ \(B \subseteq A\) であるならば、\(A=B\) です:\(A \subseteq B \quad \text{かつ} \quad B \subseteq A \quad \rightarrow \quad A = B\)
包含関係の視覚的理解:ベン図
ベン図は、集合の包含関係を視覚的に理解するための有力なツールです。たとえば、集合 \(A\) が集合 \(B\) に含まれる場合、ベン図では次のように表されます:
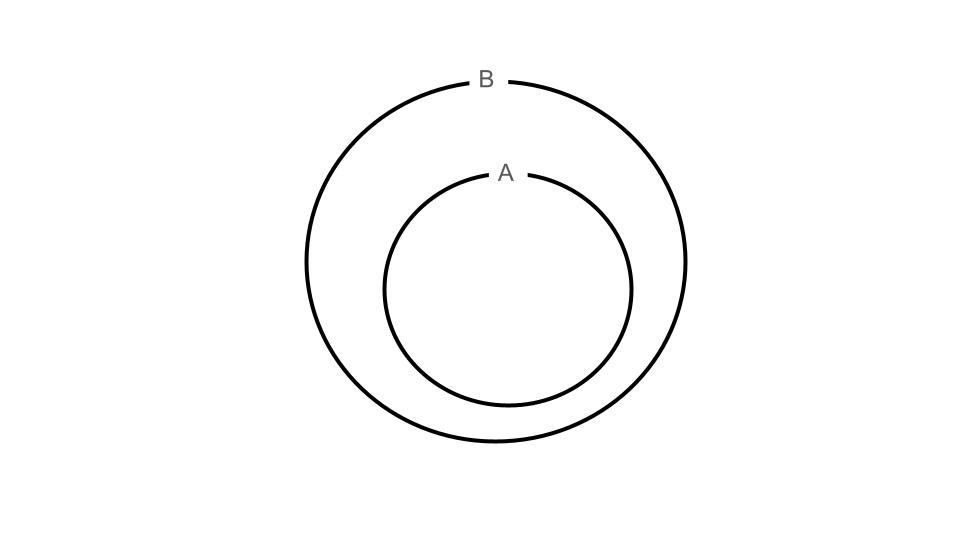
ここでは、円で表された集合 \(A\) が、より大きな集合 \(B\) の内部に完全に含まれています。このように、ベン図を使うことで、集合の関係を視覚的に捉えやすくなります。
集合の相等と包含関係
集合 \(A\) と集合 \(B\) が等しいというのは、次の条件が成立する場合です:\(A = B \leftrightarrow A \subseteq B \quad \text{かつ} \quad B \subseteq A\)
すなわち、集合 \(A\) と集合 \(B\) が等しいためには、すべての \(A\) の要素が \(B\) に含まれていると同時に、すべての \(B\) の要素が \(A\) に含まれている必要があります。これにより、両方の集合が同じ要素を持っていることが確認されます。
このことは、相等の定義を包含関係の対称性として理解することができます。つまり、集合が等しいということは、双方向の包含関係が成り立つことに他なりません。
具体例: もし \(A = \{1, 2, 3\}\) であり、\(B = \{1, 2, 3\}\) ならば、\(A\) と \(B\) は同じ要素を持っているため、\(A=B\) です。この場合、\(A \subseteq B\) かつ \(B \subseteq A\) が成立します。
包含関係と相等の例
具体的な例で考えてみましょう:
- 例 1:包含関係が成立するが、相等でない場合
集合 \(A = \{1, 2\}\) と集合 \(B = \{1, 2, 3\}\) を考えます。この場合、\(A \subseteq B\) ですが、\(A \neq B\) です。\(B\) には \(A\) にない要素 \(3\) が含まれているため、\(A\) は \(B\) の真部分集合です。 - 例 2:相等の成立
集合 \(A = \{a, b\}\) と \(B = \{b, a\}\) を考えます。集合において順序は重要ではないため、\(A = B\) です。この場合、\(A \subseteq B\) かつ \(B \subseteq A\) が同時に成り立ち、両者は等しい集合となります。
応用例
包含関係は、集合論に限らず、数学全般において非常に広く応用されます。具体例をいくつか挙げます。
- 数の範囲と包含関係
例えば、自然数の集合 \(\mathbb{N}\) 、整数の集合 \(\mathbb{Z}\) 、有理数の集合\(\mathbb{Q}\)、実数の集合\(\mathbb{R}\)、複素数の集合\(\mathbb{C}\)について、次のような包含関係が成り立ちます:\(\mathbb{N} \subset \mathbb{Z} \subset \mathbb{Q} \subset \mathbb{R} \subset \mathbb{C}\)、自然数 \(\mathbb{N}\) は整数 \(\mathbb{Z}\) に含まれ、整数は有理数 \(\mathbb{Q}\) に含まれるという具合に、包含関係が続きます。 - 幾何学における図形の包含関係
例えば、正方形は長方形の部分集合とみなすことができます。すべての正方形は長方形ですが、すべての長方形が正方形であるわけではありません。この関係は図形の分類や性質を考える上で重要です。
部分集合の応用:冪集合
ある集合 \(A\) のすべての部分集合の集合を、その集合の冪集合と呼びます。冪集合は、記号で \(\mathcal{P}(A)\) と表されます。たとえば、集合 \(A = \{1, 2\}\) の冪集合は次のようになります:\(\mathcal{P}(A) = \{\emptyset, \{1\}, \{2\}, \{1, 2\}\}\)
ここで、\(\emptyset\) は空集合で、すべての集合の部分集合です(空集合はすべての集合の部分集合であるという性質があります)。
まとめ
集合の包含関係は、数学の多くの分野で基本的な役割を果たす重要な概念です。集合の間の部分集合としての関係を正確に理解することで、集合論だけでなく、代数や解析、幾何学などさまざまな分野において論理的な基盤を構築できます。
問題
以下の二つの集合\(A, B\)の包含関係を考えよ。
(1) \(A=\{1, 2, 3, 4, 5\}, B=\{3, 4\}\)
(2) \(A=\{n\in \mathbb{N}|2 < n <8\}, B=\{n\in \mathbb{N}|3 \leq n \leq 8\}\)
参考文献
参考文献を紹介します。
以下はアフィリエイトリンクです。