数学の学び直しの記事です.
本記事では,ベクトルの定義について説明します.
ベクトルの定義
ベクトルとは,有向線分とも呼ばれ,大きさと方向をもつ量といわれます.
自然数や実数などは大きさをもつ量で,スカラーとよばれます.
スカラーとベクトルは対応しているので,セットで覚えるとよいでしょう.
まずは,大きさと方向をもつ量としてのベクトルに慣れましょう.
ベクトルはある長さをもった矢印として図示されます(下図参照).
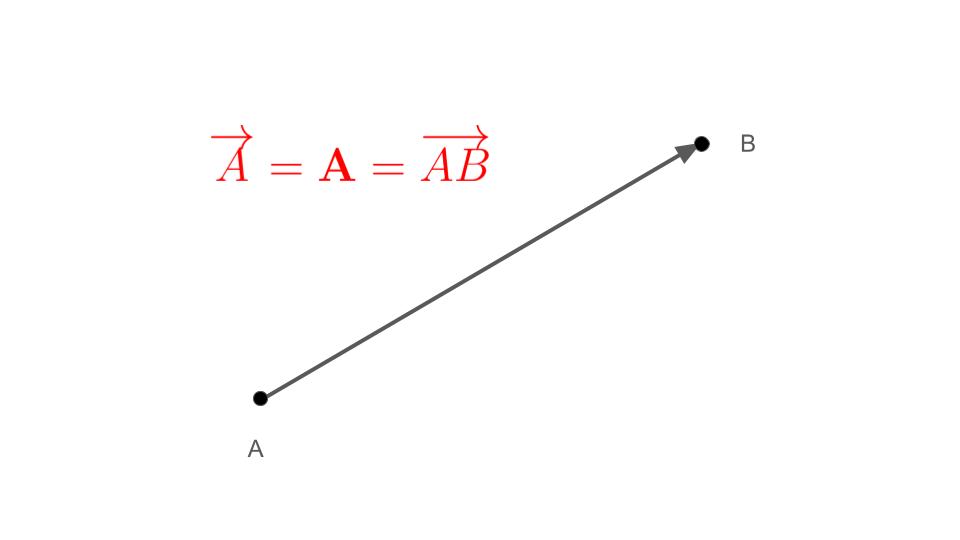
上図におけるベクトルは\(\overrightarrow{A}\)とも\(\mathbf{A}\)ともかきますが,大学以降では\(\mathbf{A}\)とかく場合が多いようです.
他方で,始点と終点を利用して\(\overrightarrow{AB}\)とも書きます.
ベクトルの相等
方向と大きさがそれぞれ等しい場合,2つのベクトルは等しいです.
平行四辺形ABCDを考えますと,\(\overrightarrow{AB}=\overrightarrow{DC}\)となります(下図参照).
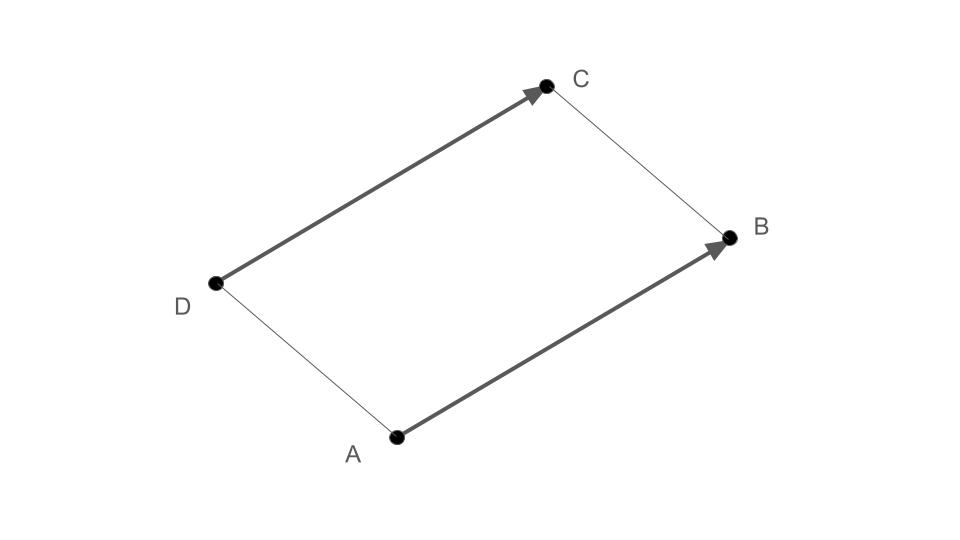
ベクトルとしては,平行移動して重なるベクトルは等しいことになります.
ベクトルの成分
座標系が与えられている場合,ベクトルを成分で表示することができます(下図参照).
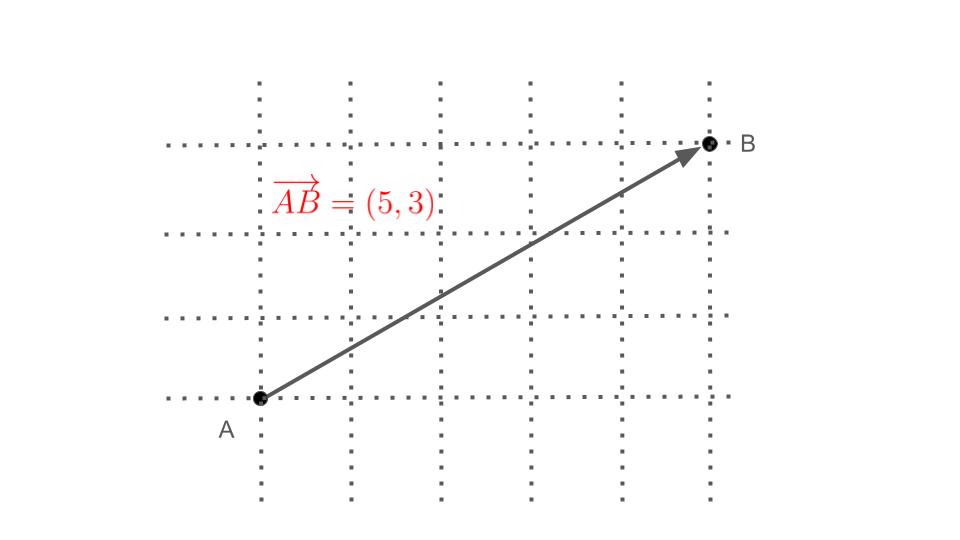
複数の座標系を考察する場合は成分表示は不向きです.
ベクトルの基本ベクトル表示
ベクトルは,座標系の基本ベクトル(座標軸方向の長さ1のベクトル,単位ベクトル)を用いて表すことが可能です(下図参照).
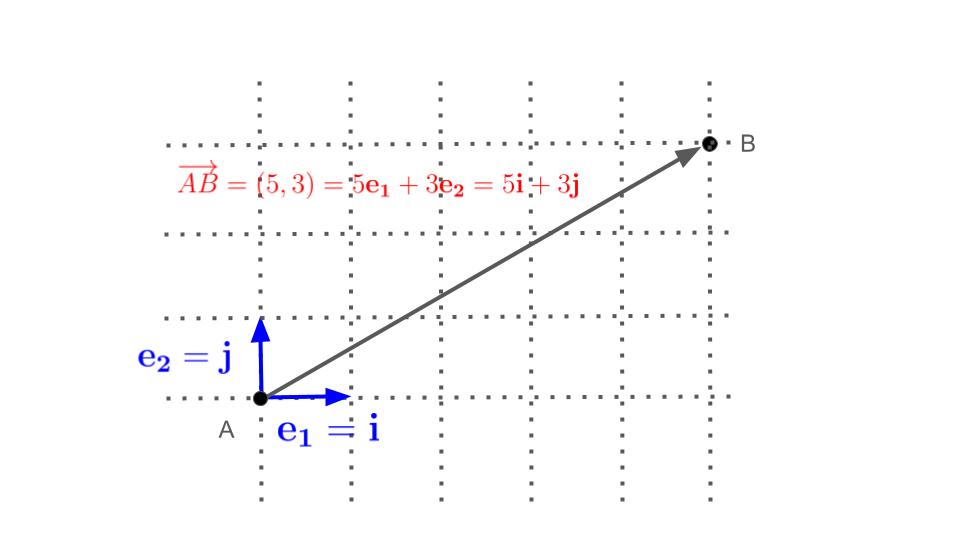
\(x\)軸方向の単位ベクトルは\(\mathbf{e}_1\)や\(\mathbf{i}\)で,\(y\)軸方向の単位ベクトルは\(\mathbf{e}_2\)や\(\mathbf{j}\)で表します.
問題
問題1
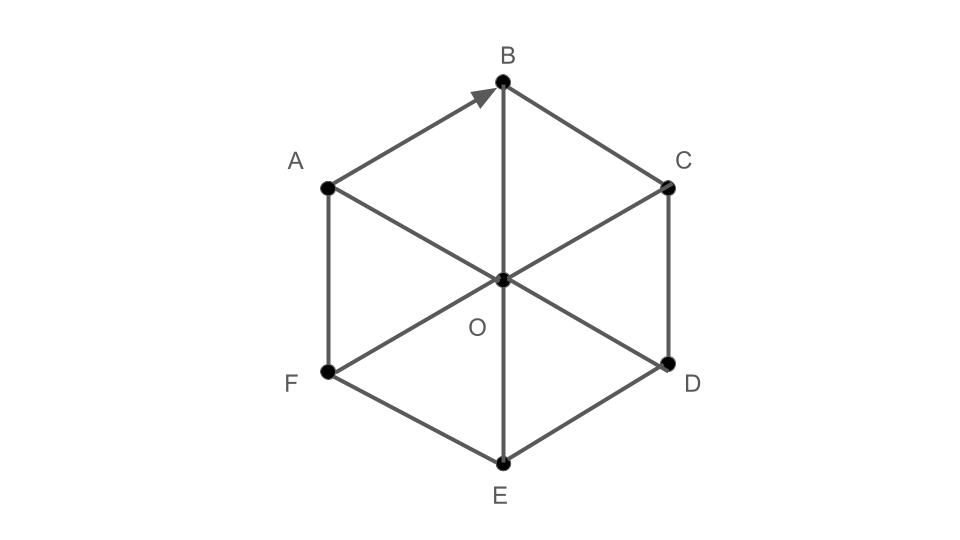
下図の正六角形において,\(\overrightarrow{AB}\)と等しいベクトルを答えよ.
問題2
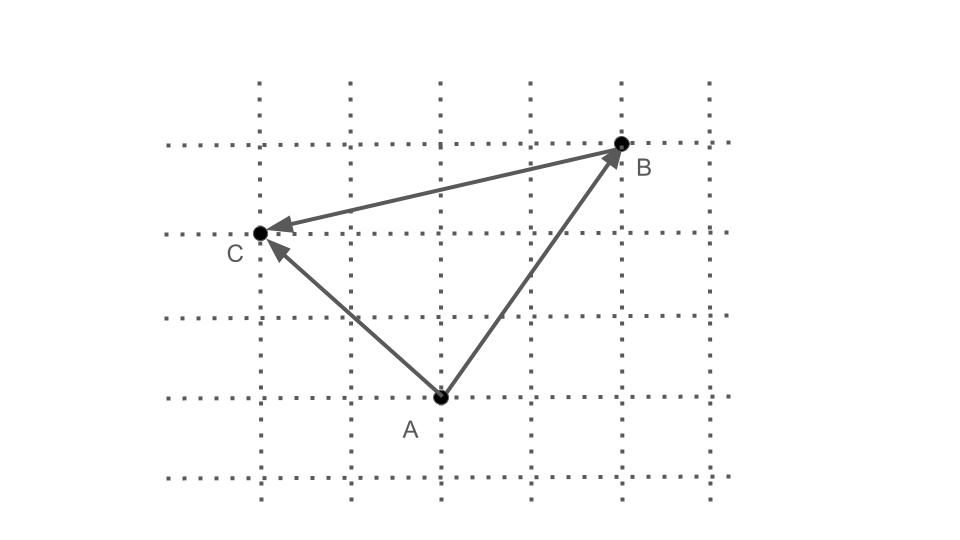
下図の\(\overrightarrow{AB}\),\(\overrightarrow{BC}\),\(\overrightarrow{AC}\)の成分を求めよ.
問題3
次の点\(A\)を始点,\(B\)を終点とするベクトル\(\overrightarrow{AB}\)の成分を求めよ.
(1) \(A:(4, 7)\),\(B:(-2, 3)\)
(2) \(A:\displaystyle\left(\frac{1}{5},\frac{2}{3}\right)\),\(B:(-2,7)\)
問題4
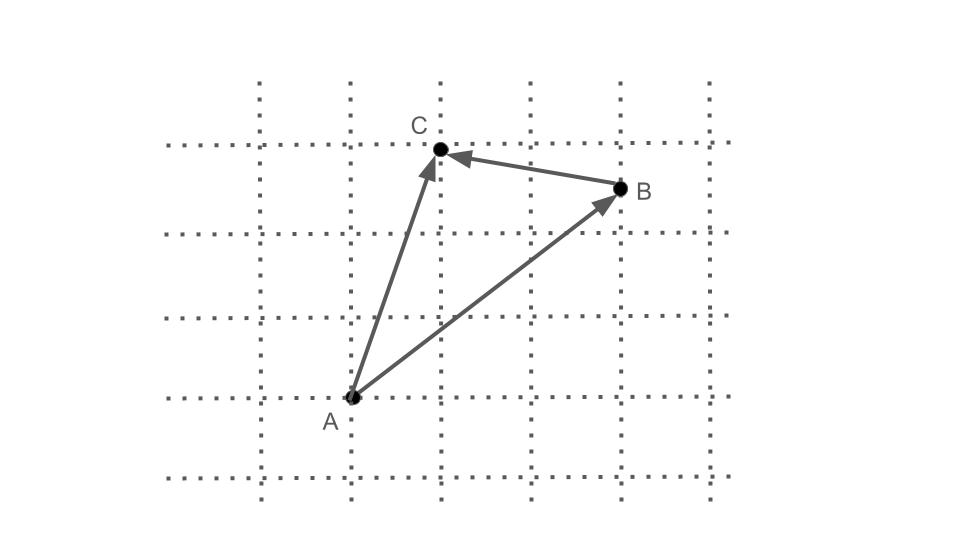
下図の\(\overrightarrow{AB}\),\(\overrightarrow{BC}\),\(\overrightarrow{AC}\)を基本ベクトル\(\mathbf{i},\mathbf{j}\)を用いて表せ.
ただし,点\(B\)は格子の中点に存在している.
解答例
問題1
\(\overrightarrow{AB}\)を平行移動して一致するベクトルを探します.
\(\overrightarrow{OC}, \overrightarrow{FO}, \overrightarrow{ED}\)
問題2
\(\overrightarrow{AB}=(2,3)\)
\(\overrightarrow{BC}=(-1,-4)\)
\(\overrightarrow{AC}=(-2,2)\)
問題3
(1) \(\overrightarrow{AB}=(-2,3)-(4,7)=(-6,-4)\)
(2) \(\overrightarrow{AB}=(-2,7)-(\displaystyle\frac{1}{5},\frac{2}{3})=(-\frac{11}{5},\frac{19}{3})\)
問題4
\(\overrightarrow{AB}=3\mathbf{i}+2.5\mathbf{j}\)
\(\overrightarrow{BC}=-2\mathbf{i}+0.5\mathbf{j}\)
\(\overrightarrow{AC}=\mathbf{i}+3\mathbf{j}\)


