物理学の学び直しのための記事です.ここでは空間内の直線や平面などの幾何学的対象の表現について解説します.
直線の表現
直線は質点のシンプルな運動の軌跡の一つです.
点\(A, B\)を通る直線を表す式は,直線上の点を\(P\)として以下のように表せます.
\(\overrightarrow{OP}=\overrightarrow{OA}+k\overrightarrow{AB}, k\in\mathbb{R}\)
\(\overrightarrow{OA}=\boldsymbol{A}, \overrightarrow{OB}=\boldsymbol{B}, \overrightarrow{OP}=\boldsymbol{P}\)とすると,
\(\boldsymbol{P}=\boldsymbol{A}+k(\boldsymbol{B}-\boldsymbol{A}), k\in\mathbb{R}\)となります(図6-1).
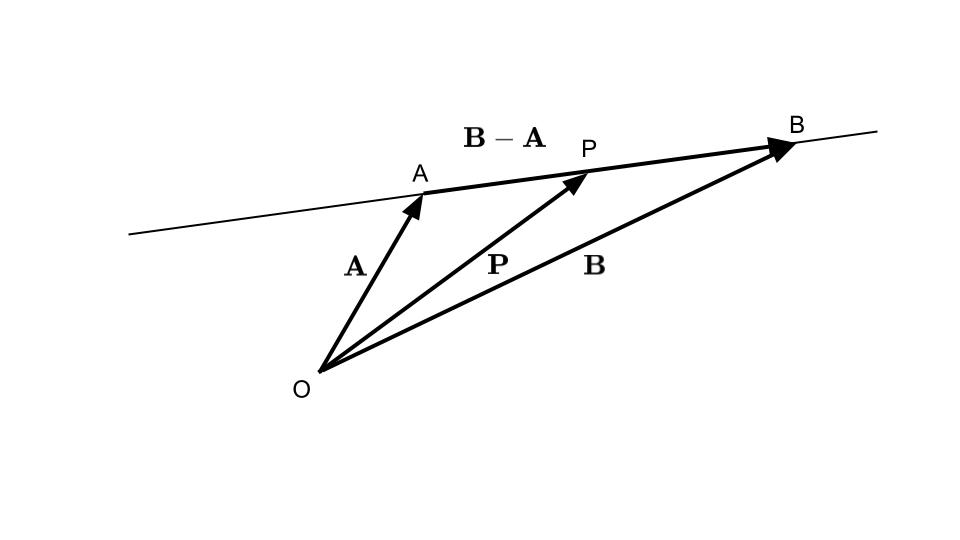
点の座標を\(A: (a_1, a_2, a_3), B: (b_1, b_2, b_3), P:(x, y, z)\)とすると,
\(\pmatrix{x \\ y \\ z}=\pmatrix{a_1 \\ a_2 \\ a_3}+k\pmatrix{b_1-a_1 \\ b_2-a_2 \\ b_3-a_3}\)
\(x=a_1+k(b_1-a_1),y=a_2+k(b_2-a_2),z=a_3+k(b_3-a_3)\)
\(a_1\neq b_1,a_2\neq b_2,a_3\neq b_3\)である場合,\(k\)を消去して
\(\displaystyle \frac{x-a_1}{b_1-a_1}=\frac{y-a_2}{b_2-a_2}=\frac{z-a_3}{b_3-a_3}\)
直線の方程式の座標表示です.
平面の表現
空間内の平面は,あるベクトルに垂直な平面として定義できます(図6-2).
点\(A\)を通り,ベクトル\(\boldsymbol{v}\)に垂直な平面上の点\(P\)は以下のように表せます.
\(\overrightarrow{AP}\cdot\boldsymbol{v}=(\boldsymbol{P}-\boldsymbol{A})\cdot\boldsymbol{v}=0\)
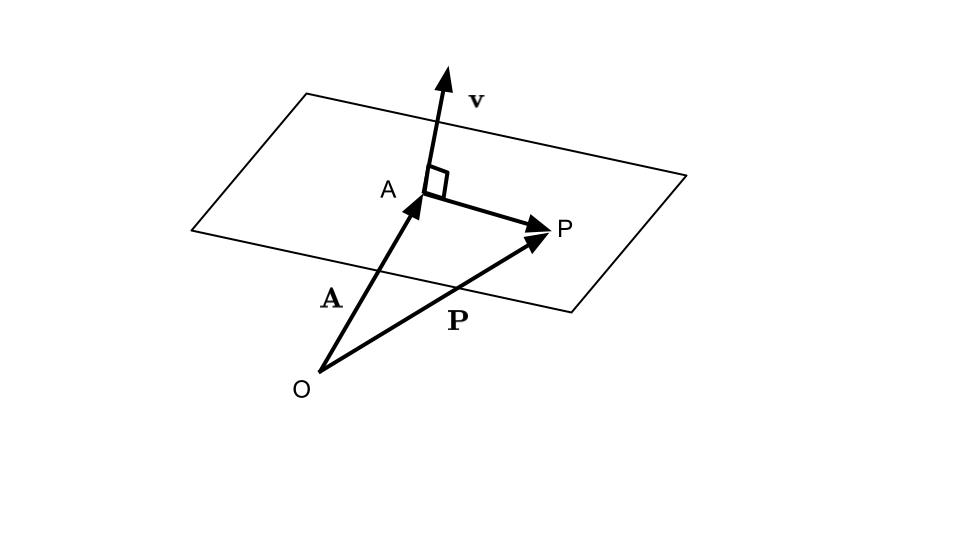
\(\boldsymbol{v}=(v_1,v_2,v_3), A:(a_1,a_2,a_3), P:(x,y,z)\)とすると,
\((x-a_1, y-a_2, z-a_3)\cdot(v_1,v_2,v_3)=0\)
\(v_1x+v_2y+v_3z=v_1a_1+v_2a_2+v_3a_3\)
平面の方程式の座標表示です.
球面の表現
球面の定義は,ある点\(A\)からの距離が一定\(r\)であることになりますので,球面上の点\(P\)は次の式で表されます(図6‐3) .
\(\mid\overrightarrow{AP}\mid^2=(\boldsymbol{P}-\boldsymbol{A})^2=r^2\)
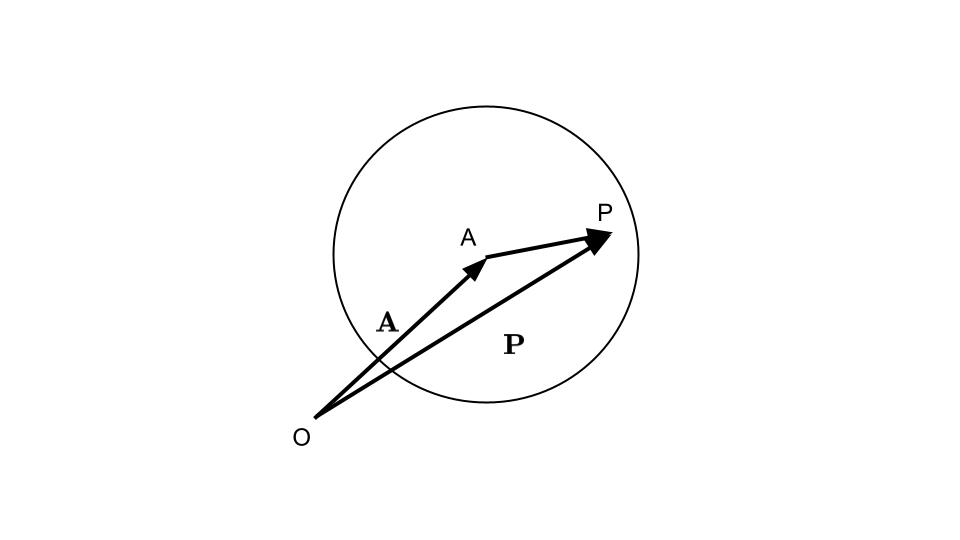
点\(A:(a_1,a_2,a_3)\),点\(P:(x,y,z)\)とすると,\((x-a_1)^2+(y-a_2)^2+(z-a_3)^2=r^2\)となります.
球面の方程式の座標表示です.
問題
問題1
同一直線上にない三点\(A:(1,2,3), B:(2,4,6), C:(3,-3,-3)\)を含む平面上の点\(P:(x,y,z)\)が満たす方程式を求めよ.
解答例
平面に垂直なベクトルを\(\boldsymbol{v}=(v_1,v_2,v_3)\)とする.
\(\boldsymbol{v}\cdot\overrightarrow{AB}=0\)から,
\(v_1+2v_2+3v_3=0\)
\(\boldsymbol{v}\cdot\overrightarrow{AC}=0\)から,
\(2v_1-5v_2-6v_3=0\)
\(v_1\)を消去して,\(9v_2+12v_3=0, v_2=-\displaystyle\frac{4}{3}v_3\)
\(v_1=-2v_2-3v_3=\displaystyle\frac{8}{3}v_3-3v_3=-\displaystyle\frac{1}{3}v_3\)
\(\boldsymbol{v}\)の一つとして\((-1,-4,3)\)とすることができる.
\(\overrightarrow{AP}\cdot\boldsymbol{v}=0\)から,
\((x-1,y-2,z-3)\cdot(-1,-4,3)=0\)
\(-x+1-4y+8+3z-9=0\)
\(x+4y-3z=0\)
参考文献
力学に関する参考文献を以下に挙げます.
アフィリエイト広告です.
戸田盛和著,『物理入門コース・力学』
藤原邦男著,『物理学序論としての力学』


