数直線と実数の大小関係について解説します.
数直線
実数を表すモデルとして,数直線をあげることができます.
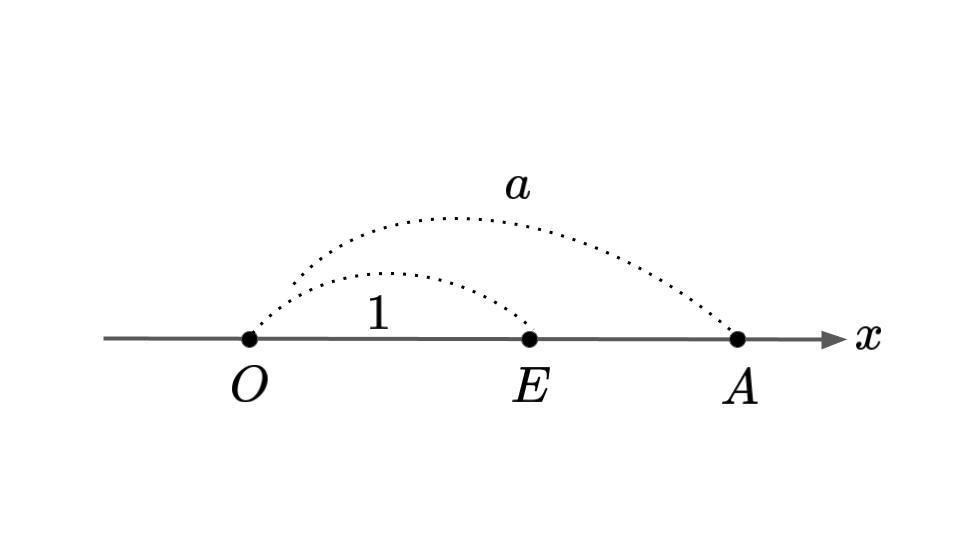
無限に伸びる直線を想定して,その直線上に一つの点をとります.
この点を原点\(O\)とします.
原点\(O\)の右側にもう一つ点をとり,これを\(E\)とします.
線分\(OE\)の長さを\(1\)と定義します.
任意の直線上の点の,原点\(O\)からの長さを実数とみなすことができます.
ただし、正負の関係があり,原点\(O\)の右側の点(\(E\)側の点)が正の数,左側の点が負の数となります(図2‐1).
整数は数直線上では原点\(O\)を含んで,長さ\(1\)で等間隔に並ぶ点列として表されます(図2‐2).

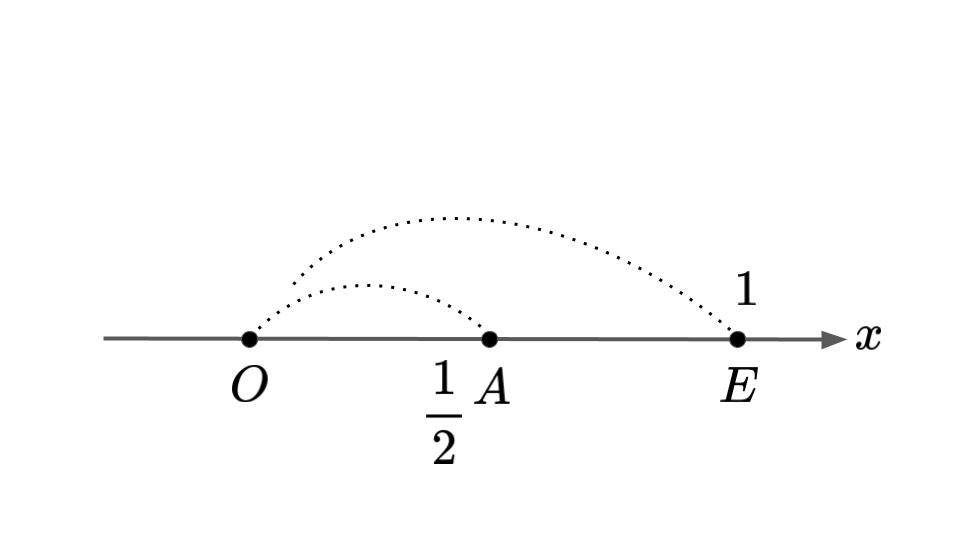
有理数(整数ではない)は,二つの整数の点の間の点として表されます.
例えば,\(\displaystyle \frac{1}{2}\)は線分\(OE\)を二等分する点\(A\)となります(図2‐3).
線分\(OE\)の間には,無限に有理数が存在することになります.
線分\(OA\)の間に\(OA\)を二等分する点\(B\)があり,さらに線分\(OB\)の間にこれを二等分する点\(C\)があり,…といった具合です.
これを有理数は数直線上に稠密に存在する,といいます.
実数の大小関係
二つの実数\(a, b\)では,次の三つの関係の内のどれかが必ず成立します.
\(a < b, \: a = b, \: a > b\)
つまり,実数には大小関係があり,大小を比較することができます.
\(a < b\)または\(a = b\)であることを,\(a \leq b\)とかきます.
相等・大小関係にはいくつかの規則がありますので,ここで簡単に触れます.
相等関係についての規則
任意の実数\(x\)に対して,\(x = x\)が成り立つ.(反射律)
任意の実数\(x, y, z\)に対して,\(x = y, y = z\)ならば\(x = z\)が成り立つ.(推移律)
任意の実数\(x, y\)に対して,\(x = y\)ならば\(y = x\)が成り立つ.(対称律)
任意の実数\(x, y\)に対して,\(x = y, y = x\)ならば\(x = y\)が成り立つ.(反対称律)
大小関係についての規則
任意の実数\(x, y, z\)に対して,\(x < y, y < z\)ならば\(x < z\)が成り立つ.(推移律)
任意の実数\(x, y, z\)に対して,\(x \leq y, y \leq z\)ならば\(x \leq z\)が成り立つ.(推移律)
任意の実数\(x, y\)に対して,\(x \leq y, y \leq x\)ならば\(x = y\)が成り立つ.(反対称律)
これらの中で推移律と反対称律は,証明問題や極限を求める問題で有用であることがあります.
不等式と加法・乗法
不等式と加法・乗法の関係を簡単に見ていきます.
不等式\(a < b\)の両辺に\(c\)を加えてもそのまま成立します.
\(a, b, c \in \mathbb{R}, a < b \Leftrightarrow a+c < b+c\)
この関係から,\(a > 0 \Leftrightarrow a-a > -a \Leftrightarrow 0 > -a\)となります.
\(a, b\)が正ならば\(ab\)も正です.
\(a, b \in \mathbb{R}, a\geq0, b\geq0 \Rightarrow ab\geq0\)
この関係から,\(a \in \mathbb{R}, a^2 = (-a)^2 \geq 0\)となります.
参考文献
解析学に関する参考文献を以下に挙げます.
アフィリエイト広告です.
松坂和夫著,『解析入門』
 |
新品価格 |
 | 価格:3,630円 |
杉浦光夫著,『解析入門I』
 |
新品価格 |
 | 価格:2,750円 |