物理学の学び直しのための記事です.ここでは空間内の位置の記述について解説します.
位置の記述
運動について研究するためには,まずは対象である物体の位置を記述する必要があります.
位置は,三次元空間において基準点を定めて空間座標を設定し,3つの数からなる座標\((x, y, z)\)で指定します.(図5-1)
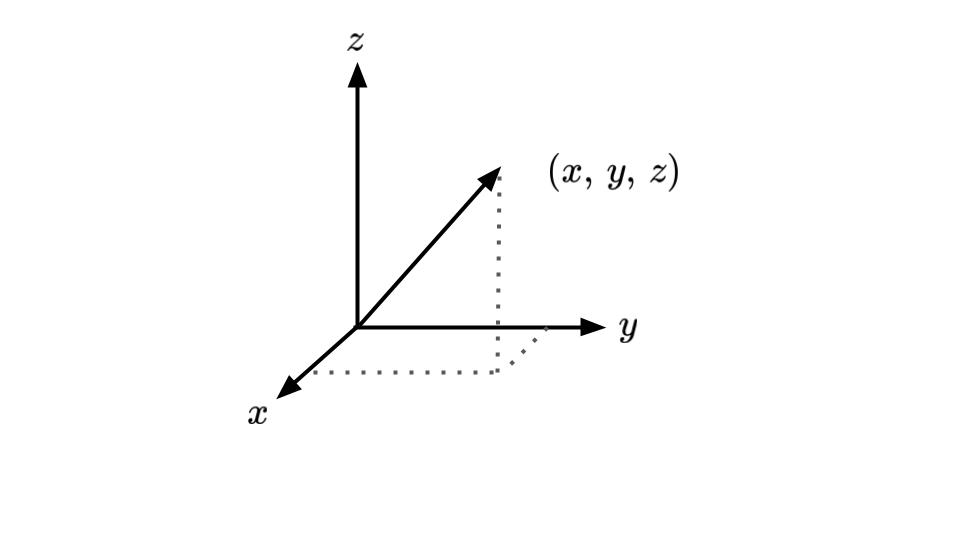
位置は,ある基準点(これを原点という)からの有向線分(向きと大きさをもつ量)である位置ベクトルによって指定できます.
位置ベクトルについて理解を深めるためには,ベクトルの性質について理解し,慣れ親しむ必要があります.
そのためのポイントとして,以下の項目を挙げます.
➀ベクトルの基礎・ベクトルの加法と定数倍
➁ベクトルの代数
➂ベクトルの大きさと内積,ベクトルのなす角
ベクトルの基礎・ベクトルの加法と定数倍
ベクトルは大きさと方向をもつ量で,矢印の方向と長さで表現できます(図5-2).
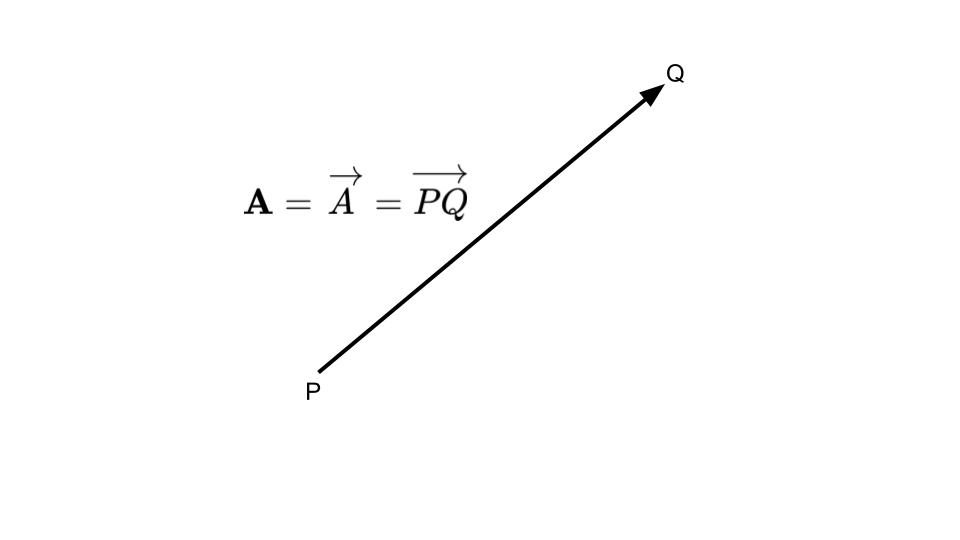
ベクトルは普通太字の文字\(\boldsymbol{A}\)で表しますが,文字の上に矢印を記す記法\(\overrightarrow{A}\)もあります.
また,始点と終点を記した記法\(\overrightarrow{PQ}\)もあります.
あるベクトルをそのままスライドして移動させた場合,つまり平行移動させた場合,もとのベクトルと移動した後のベクトルは等しいことになります.
逆に,あるベクトルを平行移動してもう一つのベクトルに重なるならば,二つのベクトルは等しいといえます(図5-3).
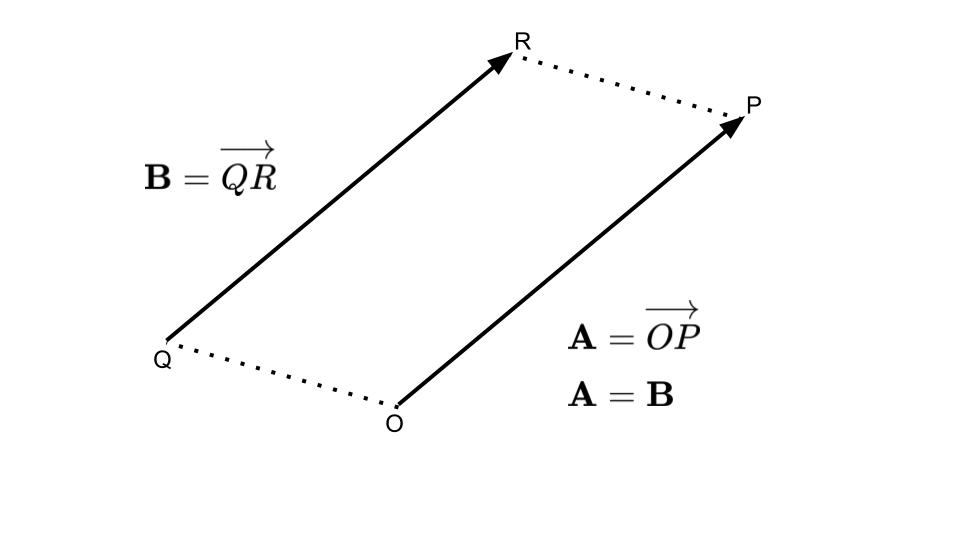
上記の図の場合,四角形\(OPRQ\)は平行四辺形をなし,\(\overrightarrow{OP}=\overrightarrow{QR}\)となります.
あるベクトル\(\boldsymbol{A}\)と同じ大きさで向きが逆のベクトルを\(-\boldsymbol{A}\)とかきます(図5‐4).
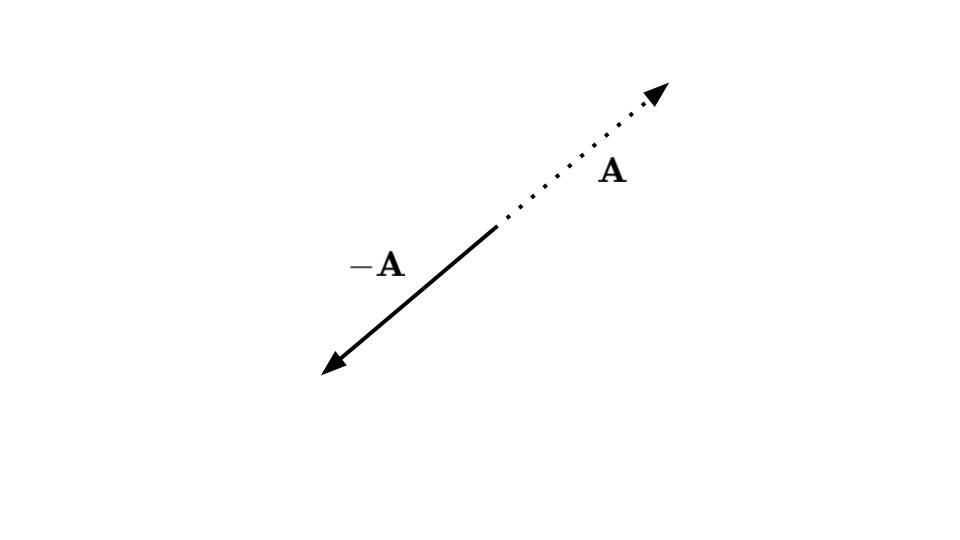
あるベクトル\(\boldsymbol{A}\)とそのマイナス\(-\boldsymbol{A}\)の和は,ゼロベクトル\(\boldsymbol{0}\)となります.
\(\boldsymbol{A}+(-\boldsymbol{A})=\boldsymbol{0}\)
ゼロベクトルは大きさが\(0\)のベクトルで,始点と終点が同一であるともいえます.
ベクトルの足し算は,下図のように平行四辺形を用いて理解できます(図5‐5).
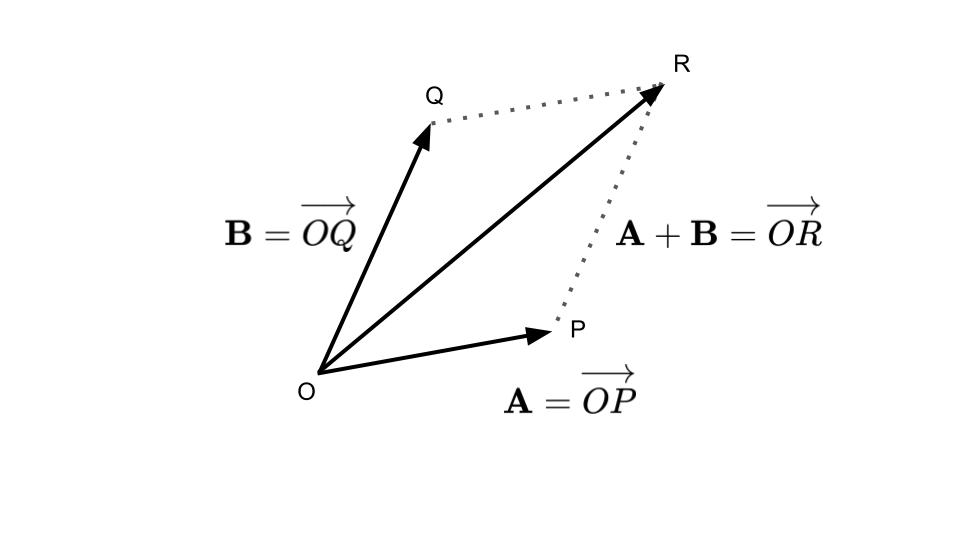
他方で,図5-6のように三角形を用いて表すこともでき,ベクトルを続けて作用させるイメージです.
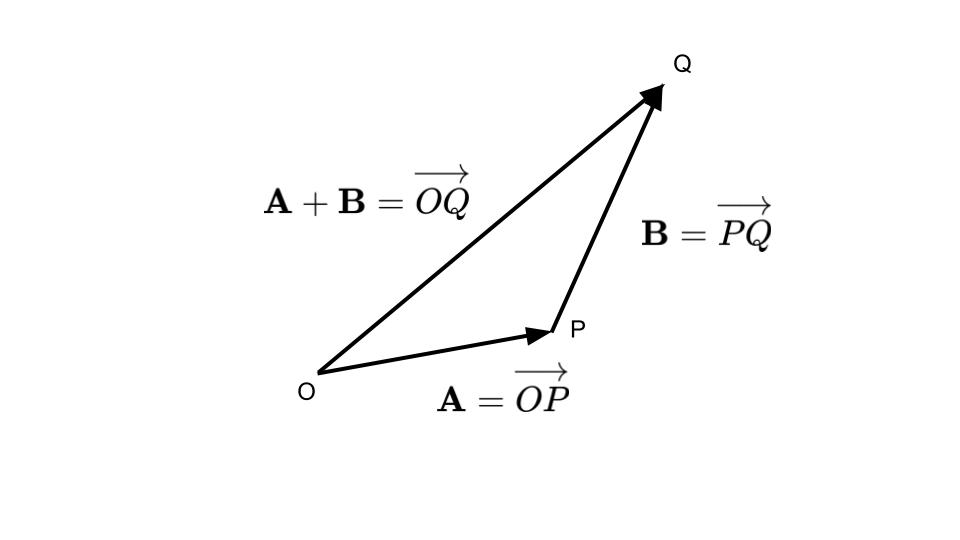
ベクトルの減法は,減ずるベクトルのマイナスを考えて,このマイナスのベクトルを加えるという形で,ベクトルの加法に帰着します.
平行四辺形による表し方(図5-7)と三角形による表し方(図5-8)があります.
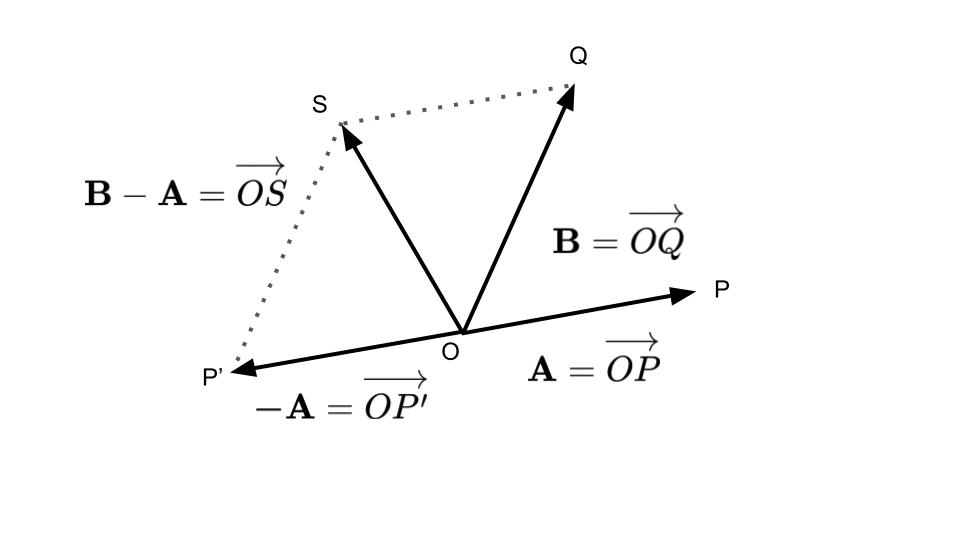
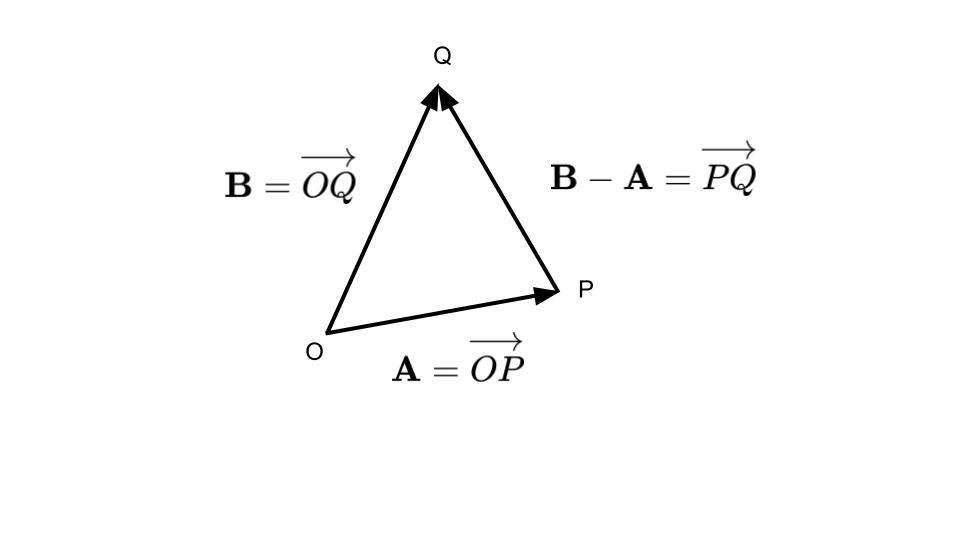
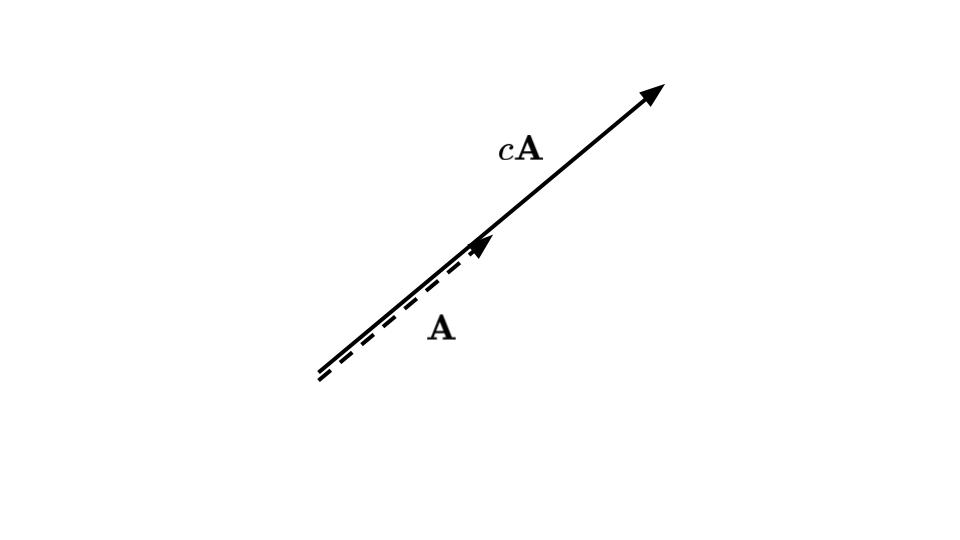
ベクトルの定数倍も,下図のように方向は同一で大きさを定数倍することにより理解できます(図5‐9).
ベクトルは空間内に座標系を設定することで,成分表示することができます(図5‐10).
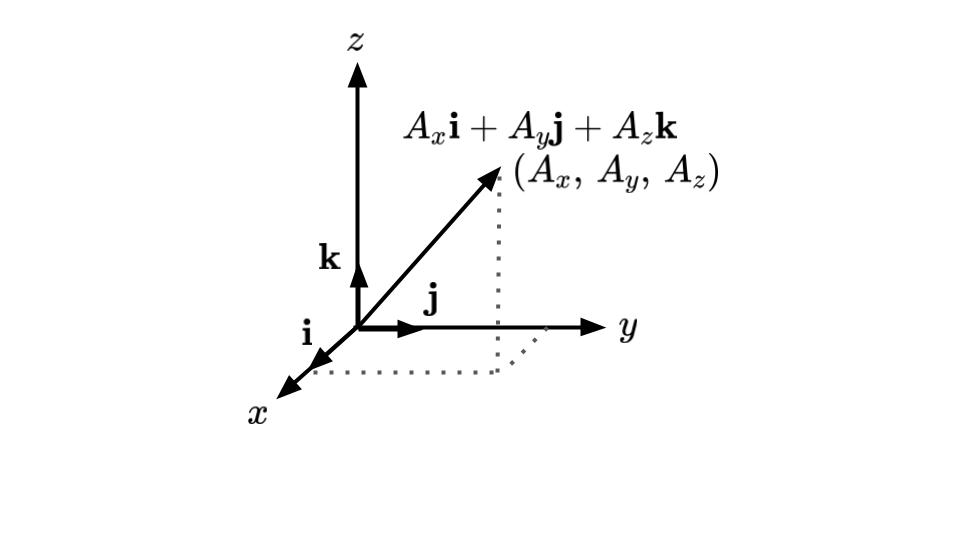
この場合,座標系の取り方は任意ですので,成分の表し方は座標系の取り方に依存することに注意が必要です.
座標軸方向の単位ベクトルを\(\boldsymbol{i}, \boldsymbol{j}, \boldsymbol{k}\)と表すと,ベクトル\(\boldsymbol{A}\)は,
\(\boldsymbol{A}=A_x\boldsymbol{i}+A_y\boldsymbol{j}+A_z\boldsymbol{k}\)
と表せます.
二つのベクトル\(\boldsymbol{A}, \boldsymbol{B}\)の和と,ベクトル\(\boldsymbol{A}\)の定数\(p\)倍は,次のように成分表示できます.
\(\boldsymbol{A}+\boldsymbol{B}=(A_x+B_x)\boldsymbol{i}+(A_y+B_y)\boldsymbol{j}+(A_z+B_z)\boldsymbol{k}\)
\(p\boldsymbol{A}=pA_x\boldsymbol{i}+pA_y\boldsymbol{j}+pA_z\boldsymbol{k}\)
つまり,ベクトルの和は,基底となる単位ベクトルが同一であるならば,成分ごとに和をとればよい,定数倍はすべての成分で定数倍すればよい,ことになります.
ベクトルでの表記は,成分ごとに書き下すより簡潔に表現され,手間も省けるのでとても便利な方法であるといえます.
ベクトルの代数
ベクトルの代数的性質として,以下の関係があります.
\(\boldsymbol A+ \boldsymbol B=\boldsymbol B+ \boldsymbol A \tag {交換法則}\)
\(\boldsymbol A+ (\boldsymbol B+ \boldsymbol C)=(\boldsymbol A+ \boldsymbol B)+ \boldsymbol C \tag{和の結合法則}\)
\(p(q \boldsymbol A) = (pq) \boldsymbol A \tag{積の結合法則}\)
\((p+q) \boldsymbol A = p \boldsymbol A + q \boldsymbol A \tag{分配法則}\)
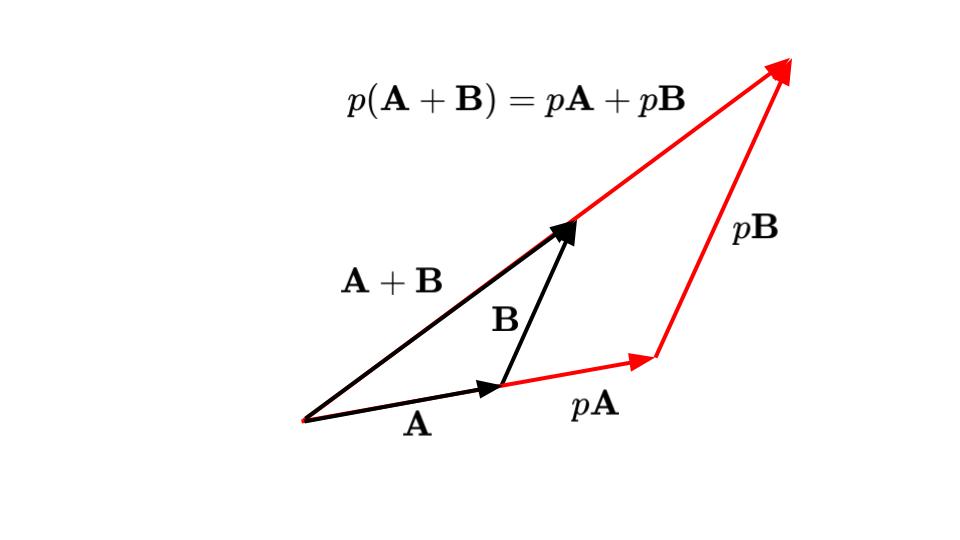
\(p(\boldsymbol A + \boldsymbol B) = p\boldsymbol A + p\boldsymbol B \tag{分配法則}\)
これらの関係は,ベクトルを図示してみると,容易に理解できます(図5‐11~図5‐13).
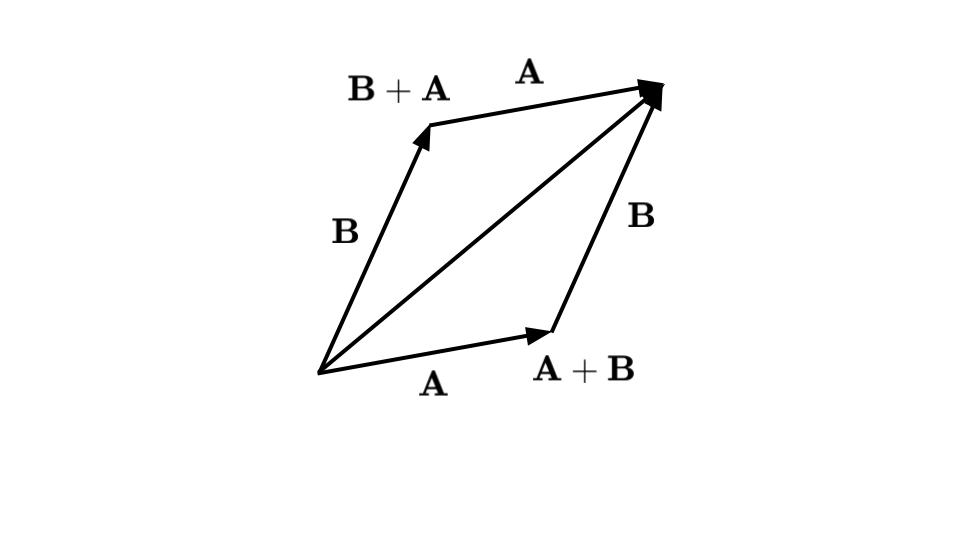
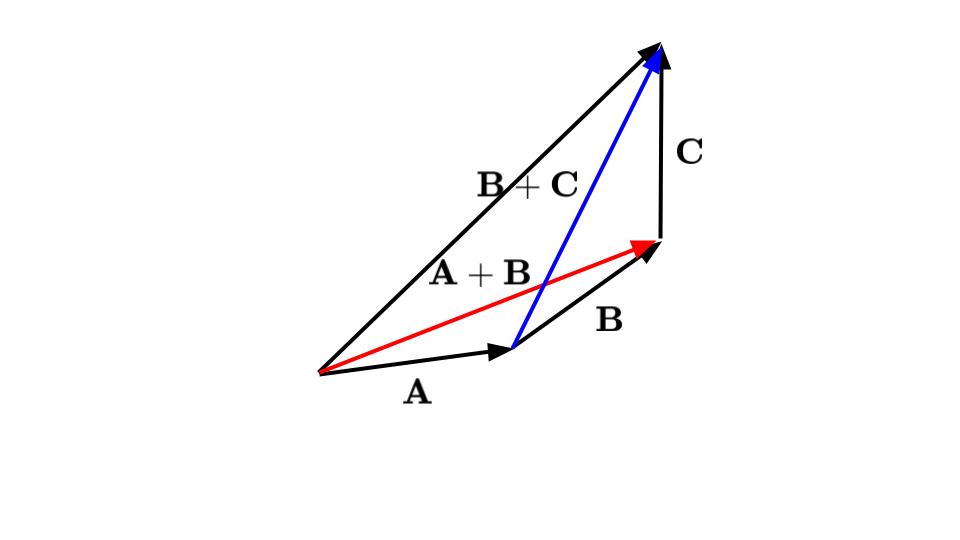
ベクトルの大きさと内積
ベクトルの大きさは有向線分の長さとなります.
ベクトルの成分が与えられていれば,三平方の定理から次式のようになります(図5‐14).
\(\mid \boldsymbol A \mid = \sqrt{A_x^2 + A_y^2 + A_z^2}\)
\(\mid \boldsymbol A \mid\)は,ベクトル\(\boldsymbol A\)の大きさを表します.

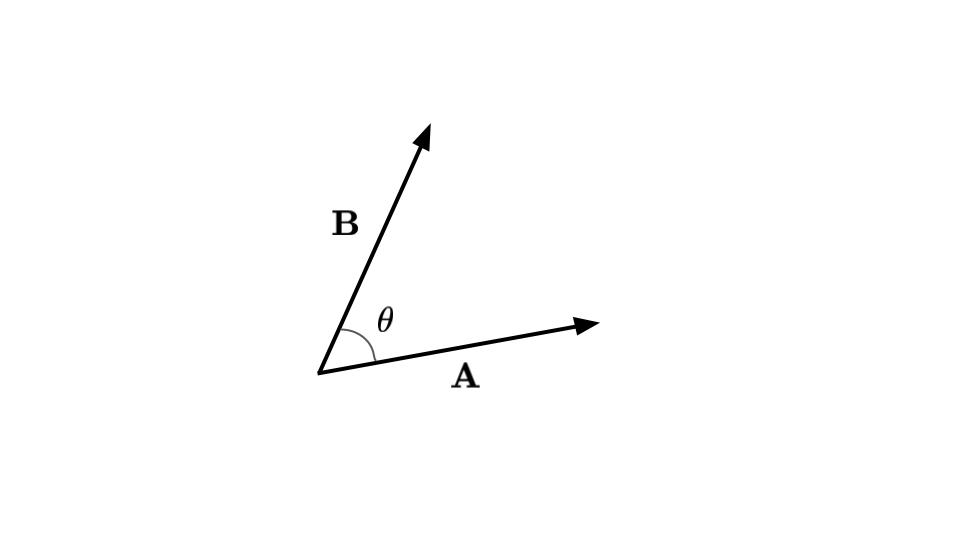
二つのベクトル,\(\boldsymbol {A}\)と\(\boldsymbol {B}\)があり,そのなす角が\(\theta\)であるとき,ベクトルの内積\(\boldsymbol {A} \cdot \boldsymbol {B}\)は以下のように定義されます(図5‐15).
\(\boldsymbol {A} \cdot \boldsymbol {B} = \mid \boldsymbol {A} \mid \mid \boldsymbol {B} \mid \cos \theta \enspace 0 \leq \theta \leq \pi \)
ベクトルの内積に関して,以下の性質があります.
\(\boldsymbol{A} \cdot \boldsymbol{B} = \boldsymbol{B} \cdot \boldsymbol{A} \tag{交換法則}\)
\(\boldsymbol{A} \cdot (\boldsymbol{B}+\boldsymbol{C}) = \boldsymbol{A} \cdot \boldsymbol{B} + \boldsymbol{A} \cdot \boldsymbol{C} \tag{分配法則}\)
\(p(\boldsymbol{A} \cdot \boldsymbol{B})=(p\boldsymbol{A})\cdot \boldsymbol{B}=\boldsymbol{A} \cdot (p\boldsymbol{B}) \tag{定数倍}\)
ベクトル\(\boldsymbol{A}\)と\(\boldsymbol{B}\)の内積が\(0\)であるとき,これらのベクトルが\(\boldsymbol{0}\)ベクトルでないならば,そのなす角が\(\displaystyle \frac{\pi}{2}\)となって,二つのベクトルは直交します.
単位ベクトル\(\boldsymbol {i}, \boldsymbol {j}, \boldsymbol {k}\)に対して,それぞれは互いに直交しているので,次の式が成り立ちます.
\(\boldsymbol {i} \cdot \boldsymbol {i} = \mid \boldsymbol {i} \mid^2 =\boldsymbol {j} \cdot \boldsymbol {j} =\mid \boldsymbol {j} \mid^2 =\boldsymbol {k} \cdot \boldsymbol {k} =\mid \boldsymbol {k} \mid^2 =1\)
\(\boldsymbol {i} \cdot \boldsymbol {j} =\boldsymbol {j} \cdot \boldsymbol {i} =\boldsymbol {j} \cdot \boldsymbol {k} =\boldsymbol {k} \cdot \boldsymbol {j} =\boldsymbol {k} \cdot \boldsymbol {i} =\boldsymbol {i} \cdot \boldsymbol {k} =0\)
単位ベクトルを利用すると,一般のベクトル\(\boldsymbol {A}\)と\(\boldsymbol {B}\)の内積は,これらの成分\((A_x, A_y, A_z)\)と\((B_x, B_y, B_z)\)を用いて以下のように表せます.
\(\boldsymbol {A} \cdot \boldsymbol {B}=(A_x \boldsymbol {i} +A_y \boldsymbol {j} +A_z \boldsymbol {k}) \cdot (B_x \boldsymbol {i} +B_y \boldsymbol {j} +B_z \boldsymbol {k})=A_xB_x +A_yB_y +A_zB_z \)
同一のベクトルの内積は,以下のようにそのベクトルの大きさの二乗になります.
\(\boldsymbol{A} \cdot \boldsymbol{A}=A_x^2+A_y^2+A_z^2=\mid \boldsymbol{A} \mid^2\)
問題
問題1
以下の二つのベクトルの和を求めよ.
(1) \(\boldsymbol{A}=2\boldsymbol{i}-3\boldsymbol{j}+\boldsymbol{k}\)
\(\boldsymbol{B}=-3\boldsymbol{i}+\boldsymbol{j}-2\boldsymbol{k}\)
(2) \(\boldsymbol{C}=-\displaystyle\frac{1}{3}\boldsymbol{i}+\displaystyle\frac{2}{5}\boldsymbol{j}-2\boldsymbol{k}\)
\(\boldsymbol{D}=\displaystyle\frac{3}{2}\boldsymbol{i}-2\boldsymbol{j}+\displaystyle\frac{1}{3}\boldsymbol{k}\)
解答例
(1) \(\boldsymbol{A}+\boldsymbol{B}\)
\(=(2\boldsymbol{i}-3\boldsymbol{j}+\boldsymbol{k})+(-3\boldsymbol{i}+\boldsymbol{j}-2\boldsymbol{k})\)
\(=-\boldsymbol{i}-2\boldsymbol{j}-\boldsymbol{k}\)
(2) \(\boldsymbol{C}+\boldsymbol{D}\)
\(=\displaystyle\left(-\frac{1}{3}\boldsymbol{i}+\frac{2}{5}\boldsymbol{j}-2\boldsymbol{k}\right)+\displaystyle\left(\frac{3}{2}\boldsymbol{i}-2\boldsymbol{j}+\frac{1}{3}\boldsymbol{k}\right)\)
\(=\displaystyle\left(-\frac{1}{3}+\frac{3}{2}\right)\boldsymbol{i}+\left(\frac{2}{5}-2\right)\boldsymbol{j}+\left(-2+\frac{1}{3}\right)\boldsymbol{k}\)
\(=\displaystyle\frac{7}{6}\boldsymbol{i}-\frac{8}{5}\boldsymbol{j}-\frac{5}{3}\boldsymbol{k}\)
問題2
点\(P(x_1,y_1,z_1)\)と点\(Q(x_2,y_2,z_2)\)がある.
ベクトル\(\overrightarrow{PQ}\)を上記の座標を含む位置ベクトルとして表せ.
また\(\overrightarrow{PQ}\)の大きさも求めよ.
解答例
点\(P\)の位置ベクトルは,\(\overrightarrow{OP}=x_1\boldsymbol{i}+y_1\boldsymbol{j}+z_1\boldsymbol{k}\),
点\(Q\)の位置ベクトルは,\(\overrightarrow{OQ}=x_2\boldsymbol{i}+y_2\boldsymbol{j}+z_2\boldsymbol{k}\)である.
\(\overrightarrow{PQ}=\overrightarrow{OQ}-\overrightarrow{OP}\)
\(=(x_2\boldsymbol{i}+y_2\boldsymbol{j}+z_2\boldsymbol{k})-(x_1\boldsymbol{i}+y_1\boldsymbol{j}+z_1\boldsymbol{k})\)
\(=(x_2-x_1)\boldsymbol{i}+(y_2-y_1)\boldsymbol{j}+(z_2-z_1)\boldsymbol{k}\)
\(\overrightarrow{PQ}\)の大きさ\(\mid\overrightarrow{PQ}\mid\) は,
\(\mid\overrightarrow{PQ}\mid=\sqrt{(x_2-x_1)^2+(y_2-y_1)^2+(z_2-z_1)^2}\)である.
参考文献
力学に関する参考文献を以下に挙げます.
アフィリエイト広告です.
戸田盛和著,『物理入門コース・力学』
 |
新品価格 |
 | 価格:2,420円 |
藤原邦男著,『物理学序論としての力学』
 |
新品価格 |
 | 基礎物理学1物理学序論としての力学【電子書籍】[ 藤原邦男 ] 価格:2,310円 |


